Blender 2.9 の使い方 (17) ジオメトリーノード2
Blender 3.0 のジオメトリーノードは大幅に変更されました。解説は こちら です。
Blender のジオメトリーノードのチュートリアル動画に Entagma による Blender Geometry Nodes: Vertex Normals - Alien Orb というものがあります。 複数のオブジェクトに対して、それぞれ設定したジオメトリーノードが連携して動作するアニメーションの作成方法がわかりやすく解説されています。 Blender のジオメトリーノードの利用者の増加に影響しそうな良質なサンプルであると思います。 強くおすすめします。
さて、動画を見ながらノードの全体像を理解するのは大変なので、チュートリアルに沿って実行した結果を記録しながら進めていきました。 一旦すべてのノードの働きを理解したと思うので、備忘録として解説を加えたものを公開します。
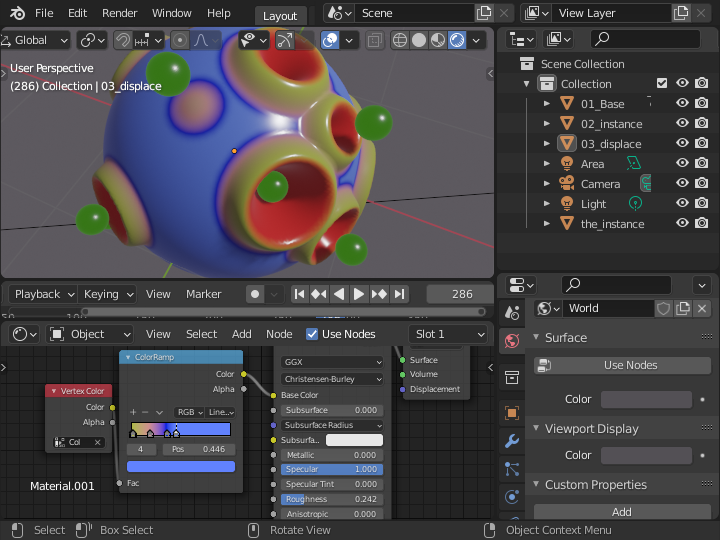
回転して広がる球体の位置
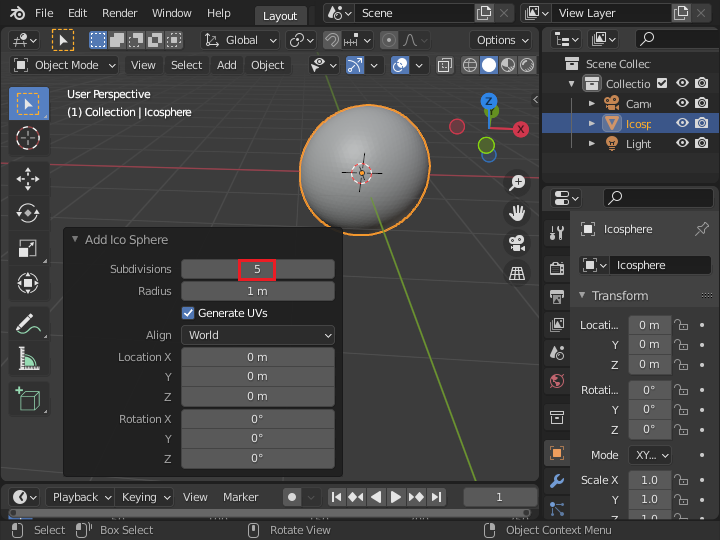
上の図の緑の球体が運動する範囲を設定するオブジェクトとして、「Add / Mesh / Ico Sphere」で球体を配置します。 あまりメッシュを細かくしなくても問題ありませんが、オリジナル を尊重して、細分化レベルを 5 にします。
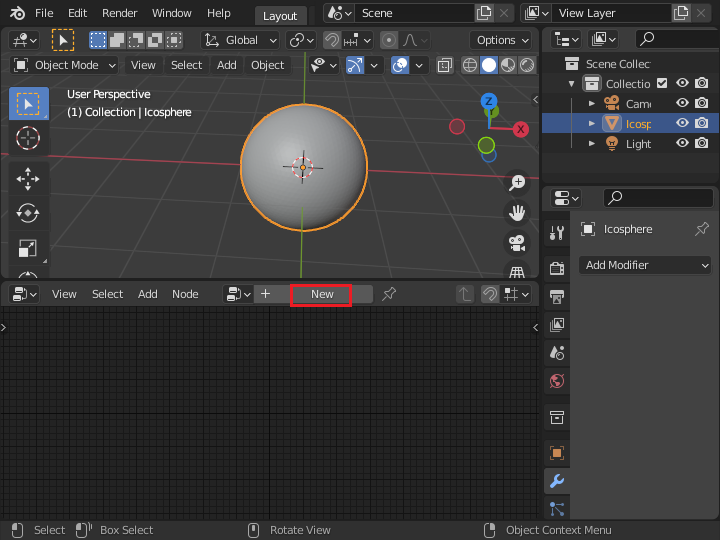
下側の領域を Geometry Node Editor にします。 この辺の画面の操作はBlender 2.8 の画面構成 を参考にしてください。 ジオメトリーノードを作成するために、ヘッダーリージョンの「New」をクリックします。
「Geometry Nodes」という名前のジオメトリーノードができました。 「Group Input」 というノードと、「Group Output」というノードが「Geometry」というソケットで接続されています。 「入力側の物体の形状を、そのまま表示側に出力する」という意味になります。 この間に色々なノードを挿入して、位置や形状を変化させていくことになります。
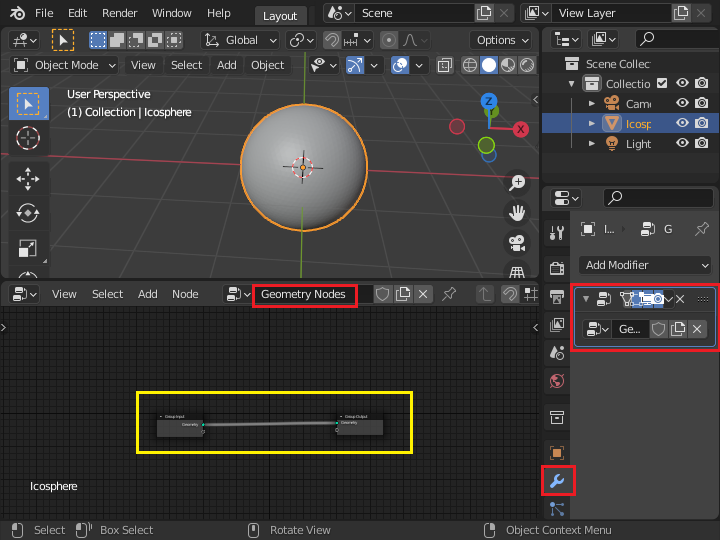
ジオメトリーノードの名前を「Base」に変更します。
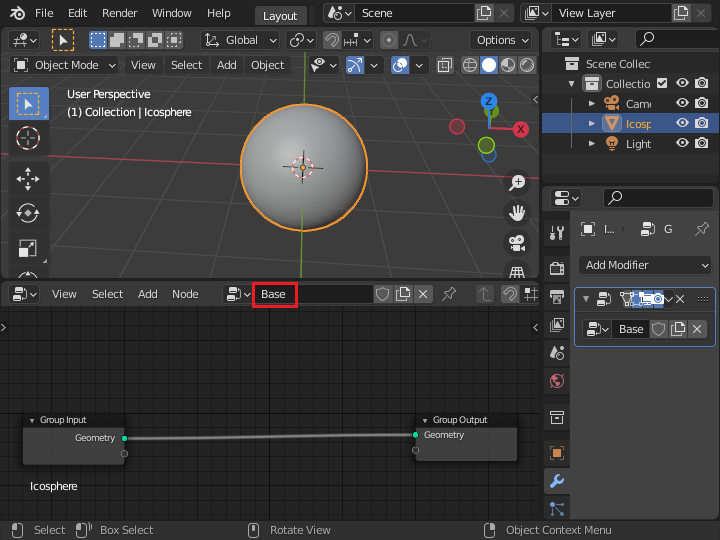
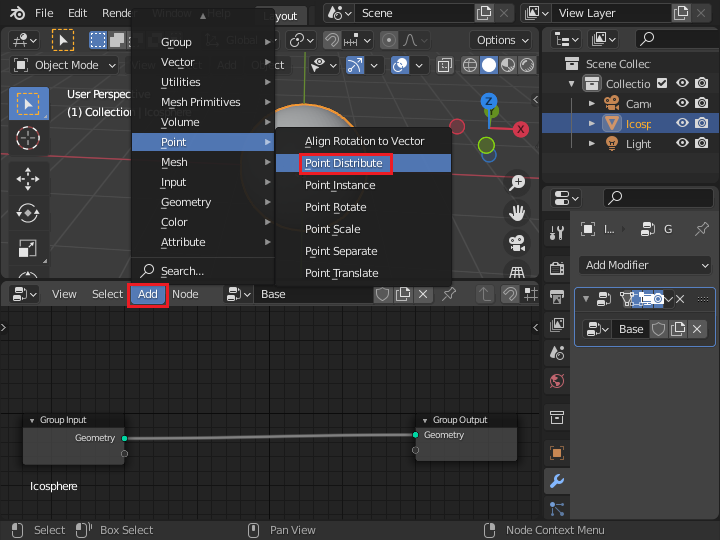
オブジェクトの中心となる点を生成するために「Point Distribute」ノードを追加します。
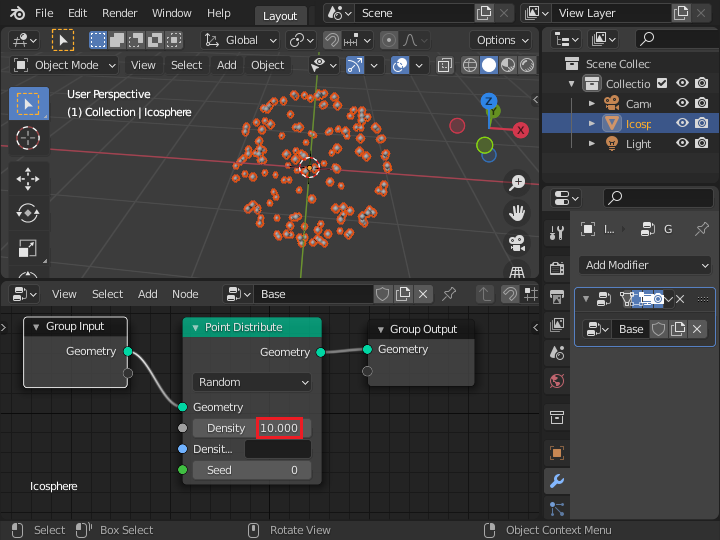
IcoSphere の形状を持つ「Group Input」ノードが「Point Distribute」ノードで複数の点に変換されるため、Ico Sphere (球体) が消えています。 Density (密度) の値を大きくすると、点の数が増えます。
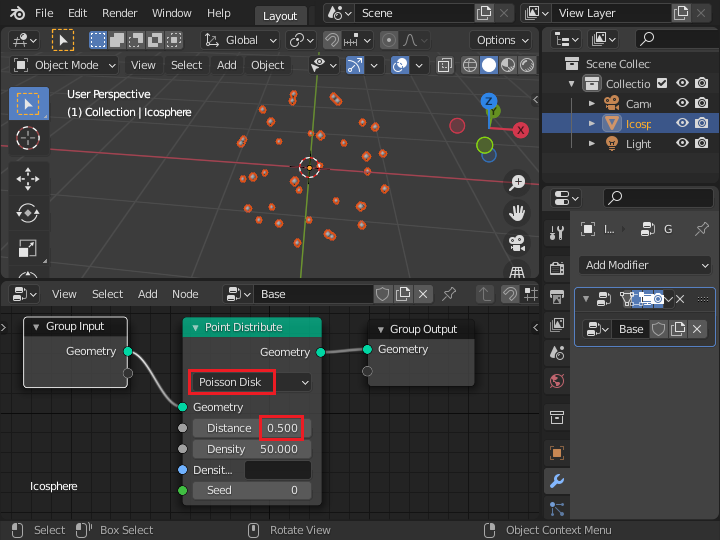
Random から Poison Disk に変更すると、Distance で指定した値より近い点が生成されなくなります。
「Add / Utilities」から「Math」ノードを追加します。
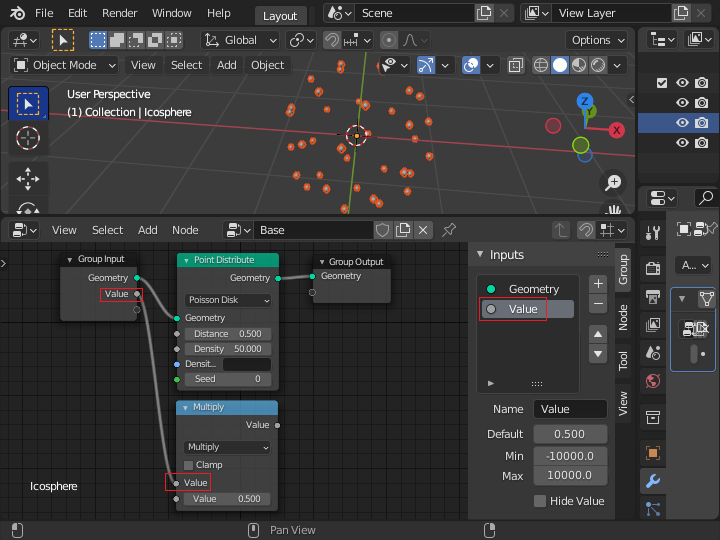
「N」キーを押してサイドバーを表示して、Inputsパネルから「Value」をクリックして名前を Frame に変更します。 ジオメトリーノードに外から与える Frame というパラメータを追加することになります。
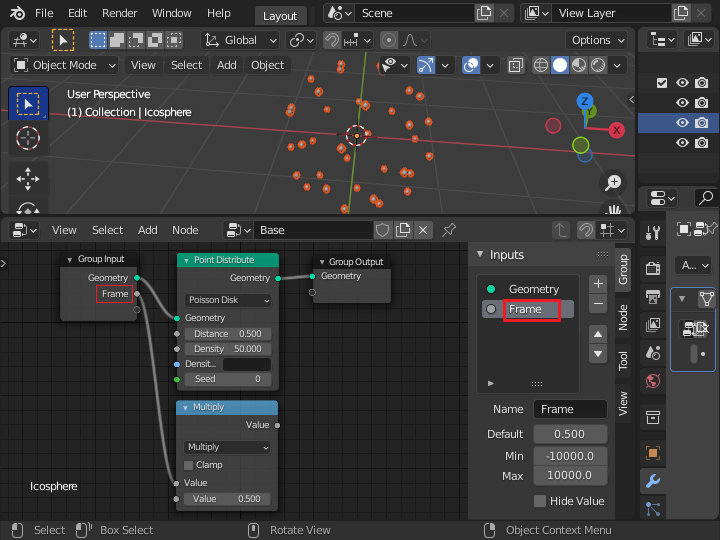
プロパティタブからジオメトリーノードモディファイアを見ると、Frame という入力パラメータが確認できます。
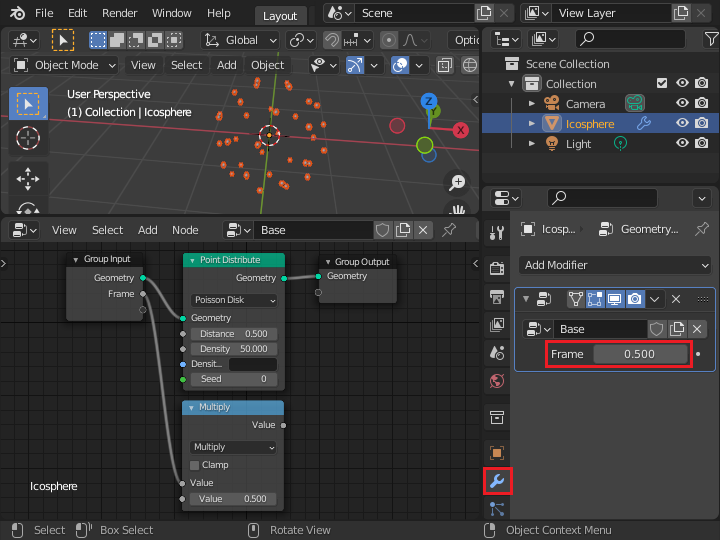
frame をドライバに設定
Frame項目の数値を入力する場所に 「#frame」と入力します。
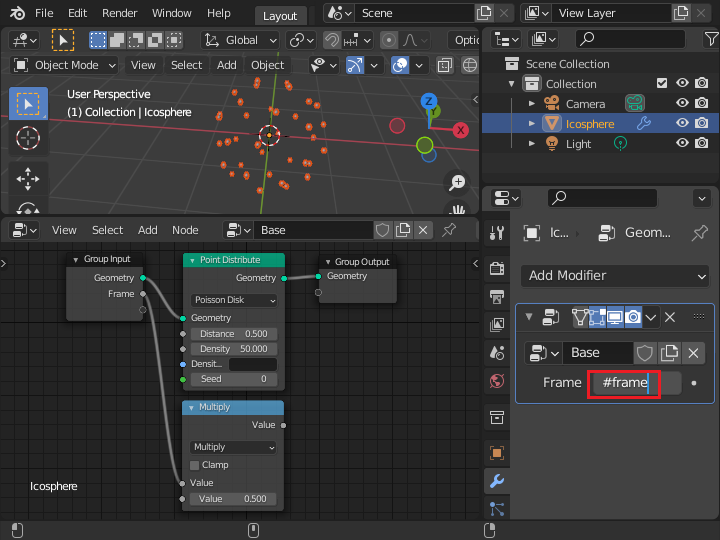
Frame項目の背景色が変化して、アニメーション実行時のフレーム数と連動 (ドライバ) することになります。 このジオメトリーノードのサンプルの心臓部となる部分で、アニメーション実行時のフレーム数からすべてのオブジェクトの運動と色の変化を求めています。 ジオメトリーノードの設定だけで、いろいろな長さのアニメーションの動きを自動的に作成できてしまいます。
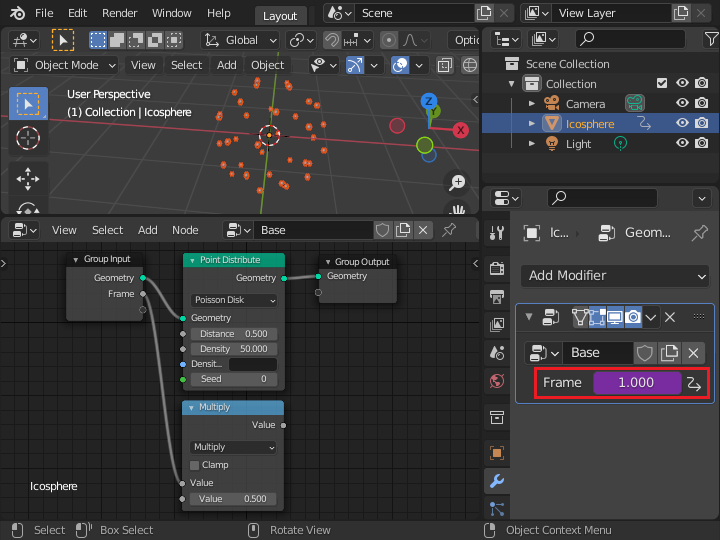
タイムラインエディタのフレーム数が、ジオメトリエディタの Frame パラメータと一致するように変化します。 アニメーションを再生すると、フレーム数がジオメトリーノードに渡って、時間が変化した場合に動作させるためのネタとして使うことができます。
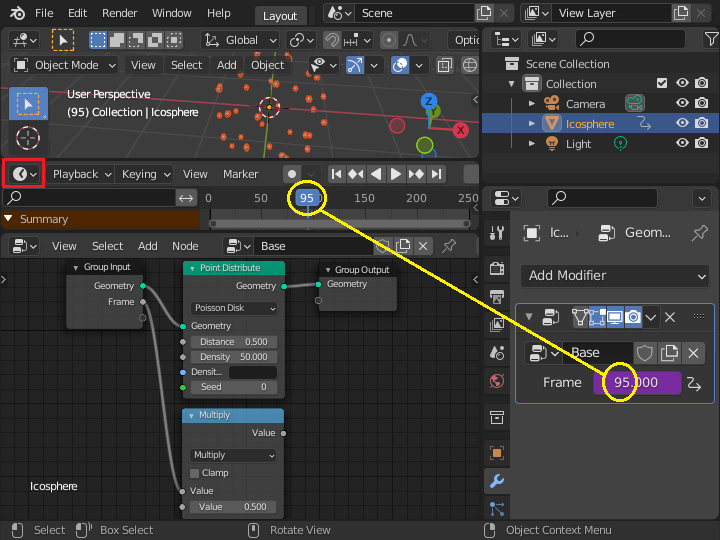
「Attribute Math」ノードを追加して、演算の種類を「Sine」としてサイン関数を指定します。
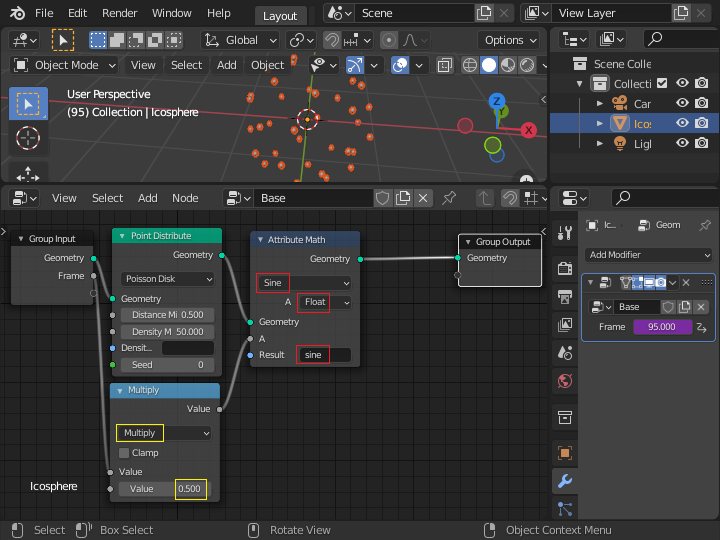
「Attribute Math」ノードをさらに追加して、演算を「Multiply」、Aの値を「normal」に設定します。 元の球体 (Ico Sphere) の表面から外側に向く、Geometryソケットから入ってくる点の位置の法線ベクトルが設定されます。
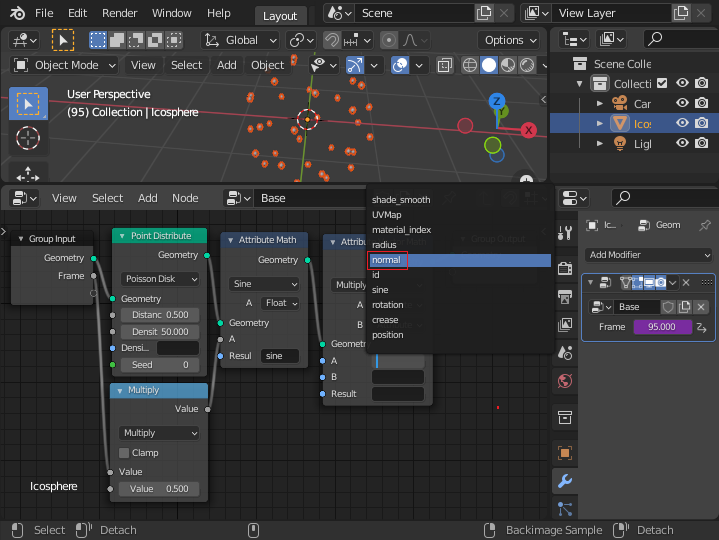
さらに、「Attribute Math」ノードの Bの値を「sine」に設定します。 結果の値を「disp」属性(変数)に設定します。 これで次のようにフレーム数に定数を乗じたもののサイン関数の結果が disp に設定されます。 フレーム数によって disp の値は ±1 の範囲で法線ベクトルに乗算されます。
disp = sin(0.5 * frame) * normal
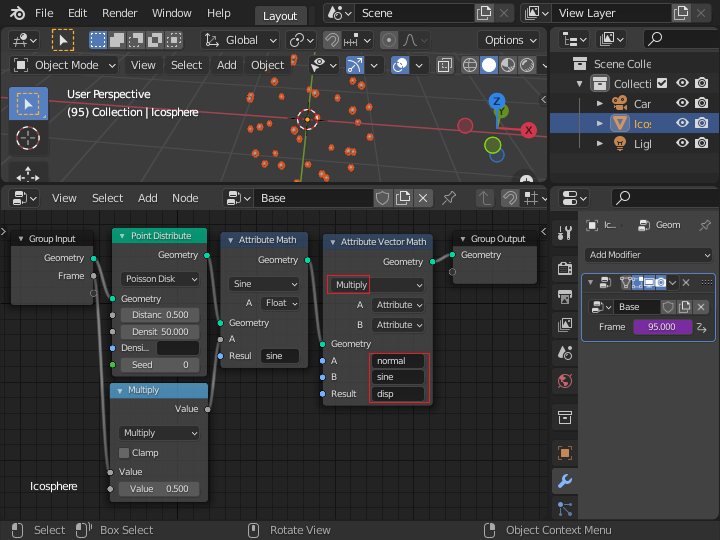
もう1つ「Attribute Math」ノードを追加して、「position」に 「disp」を加えたものを「position」に戻します。 これでフレーム数が変化すると、中心に近づいたり、離れたりする動きになります。
position = position + sin(0.5 * frame) * normal
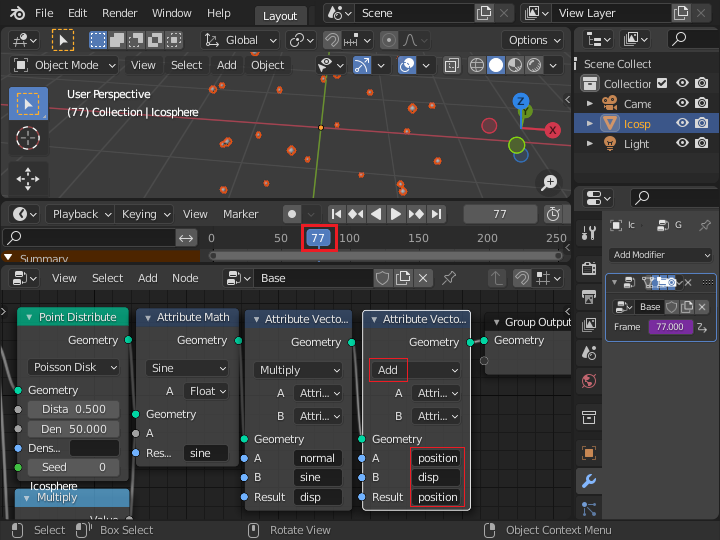
フレーム数を少し変更すると、点の位置は中心に向かって移動しています。
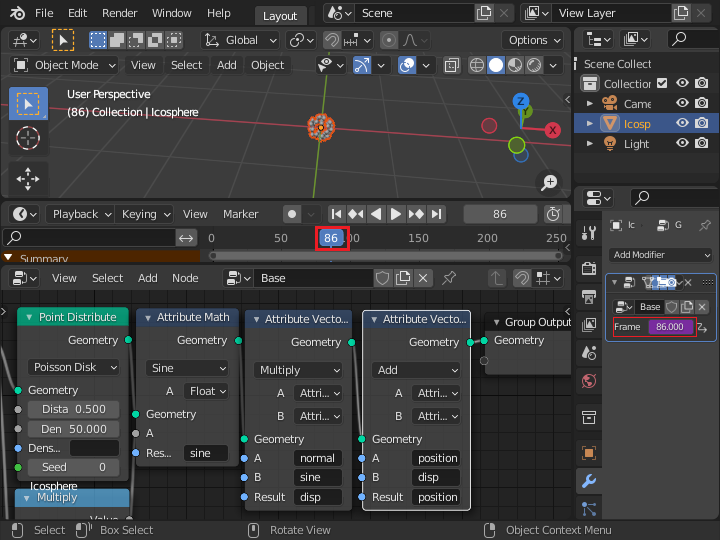
点の位置の変化はサイン関数なので ±1.0 の変化となりますが、変化量を小さくできるように、定数を乗算できるように「Attribute Math」ノードを挿入します。
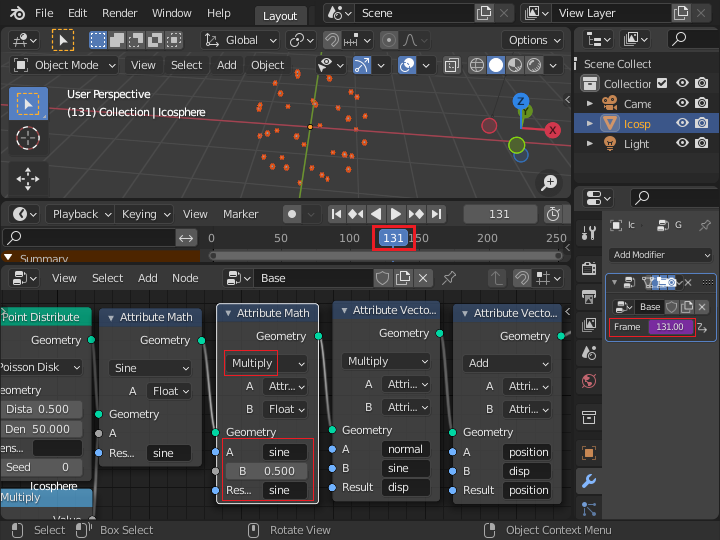
「Attribute Randomize」ノードを加えて 0 から 3.0 の範囲の乱数を rnd 属性に設定します。
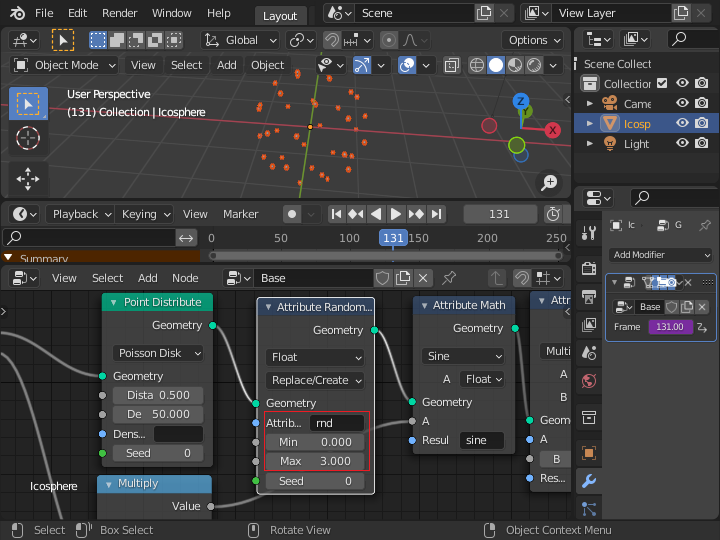
「Attribute Math」ノードを追加して乱数をフレーム数に定数をかけたものに加えます。 フレーム数がばらつくため、動きに変化が生まれます。
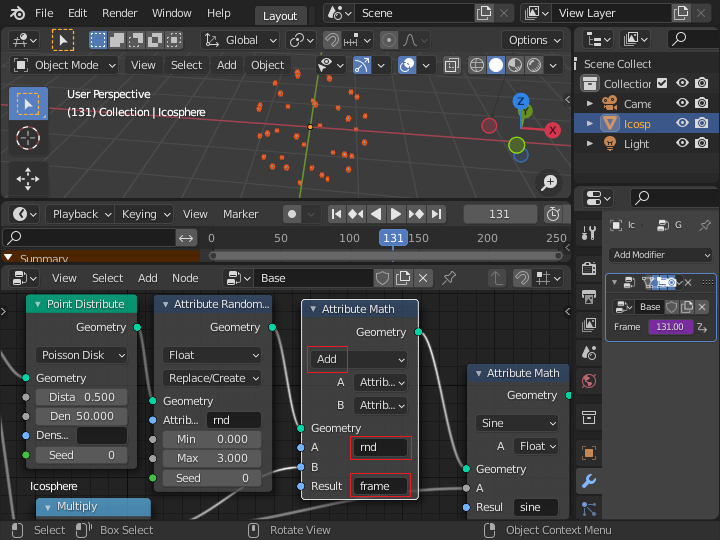
サイン関数の入力をフレーム数に乱数を加えた「frame」属性に変更すると、点の分布がばらついていることが確認できます。
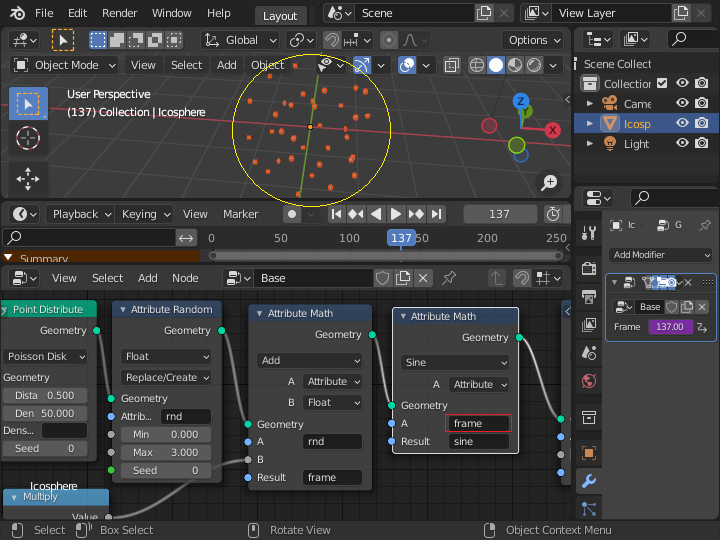
「Grouo Output」ノードの直前に「Transform」ノードを追加して、最終的に全体に回転を加えることにします。
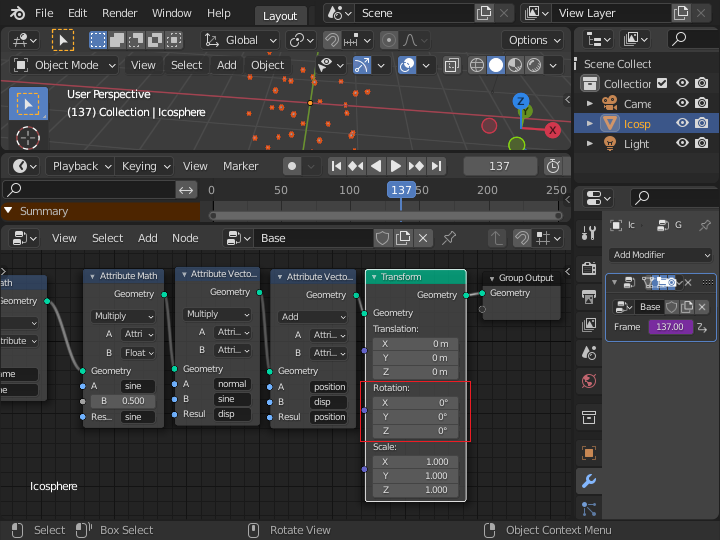
「Combine XYZ」ノードで、X、Y、Zの各軸ごとに値を設定できるようにします。
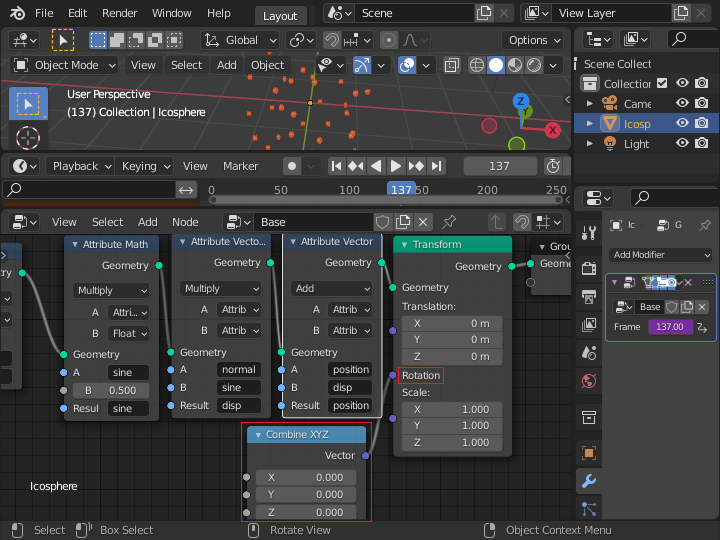
回転の範囲を計算するため、「Combine XYZ」ノードの前に「Map Range」ノードを追加します。
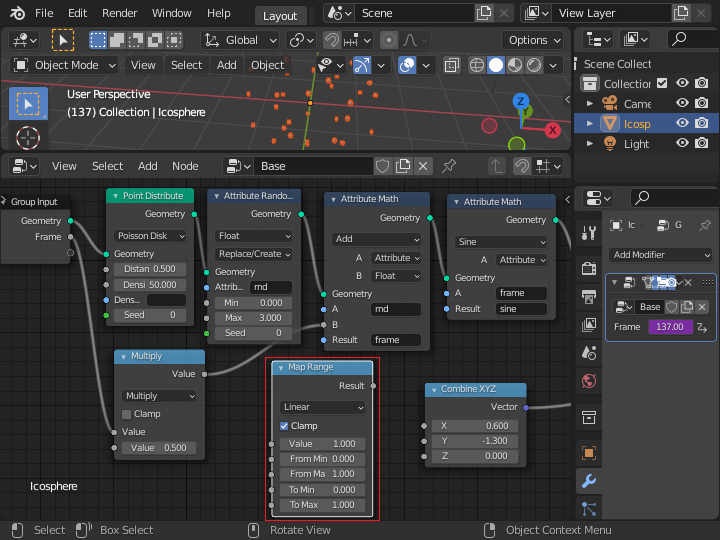
「Map Range」ノードの Value 入力は「Group Input」ノードの「Frame」から接続します。0 から 300 までのフレーム数の変化を 0 から6.28 (2pi 1回転) に変換します。 アニメーションのフレーム数が 0 から 300 まで変化する間に360度回転することになります。
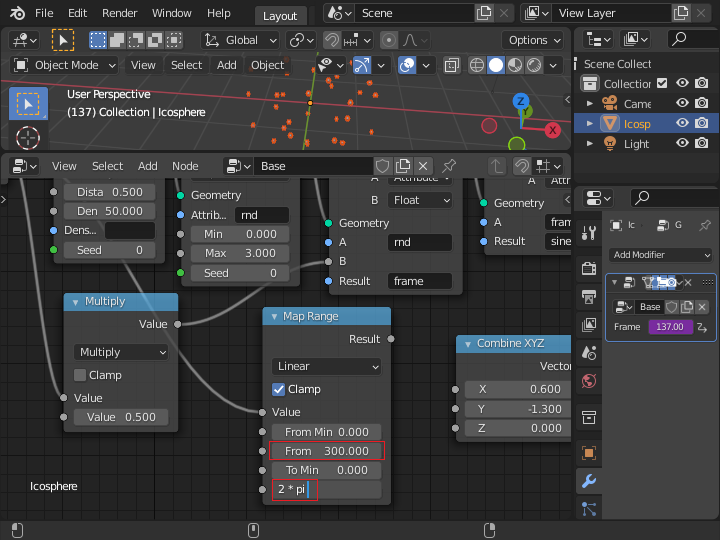
結果を「Combine XYZ」ノードのXに接続して、もう1つ「Map Range」ノードを追加します。 この「Map Range」ノードは 0 から 150 までのフレーム数の変化を 2π(1回転)に変換します。 300フレームで2回転するようになります。こちらは「Combine XYZ」ノードのZにつなぎます。
図の左端のフレーム数に最初に乗算する定数は「0.05」に変更しています。この値を小さくすると、点が広がったり集まったりする動きが遅くなります。
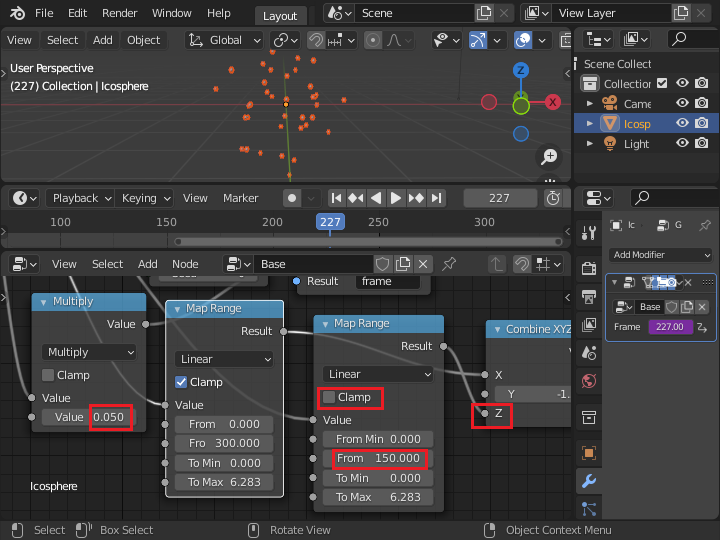
赤枠は、0 から 300 までのフレーム数の変化が、 Attribute ノードや Math ノードを介して伝わっていく様子を示しています。 下側が回転運動に関するもので、上側が法線方向の変位量 (広がったり、集まったり) に変換されます。
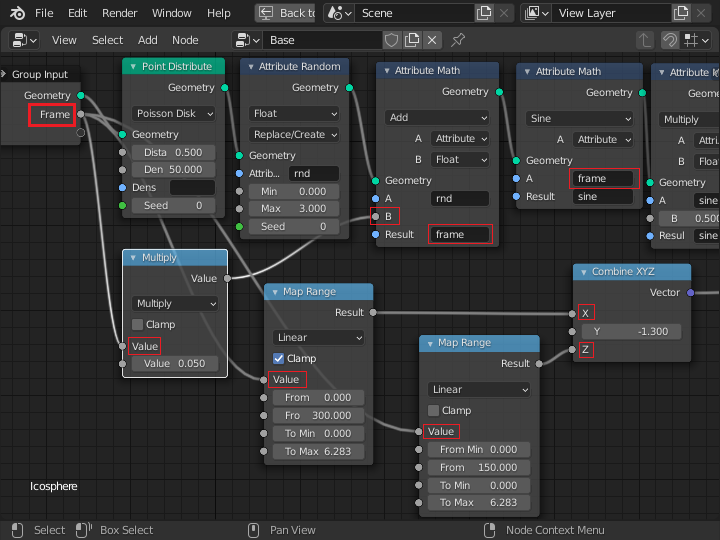
「Grouo Output」ノードで出力される周辺のノードを示します。 上側のノードで、フレーム数から計算された数値が、法線方向の変位量 (disp) となり、さらに位置情報 (position) に変換されます。
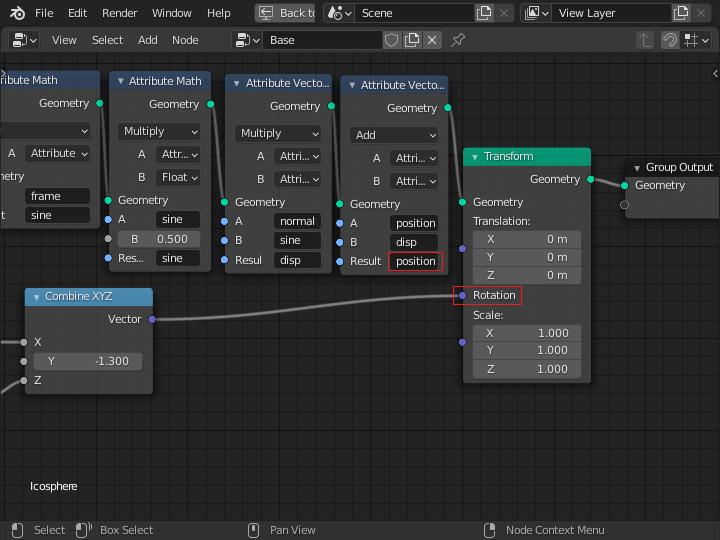
アニメーションを実行して動作を確認しましょう。
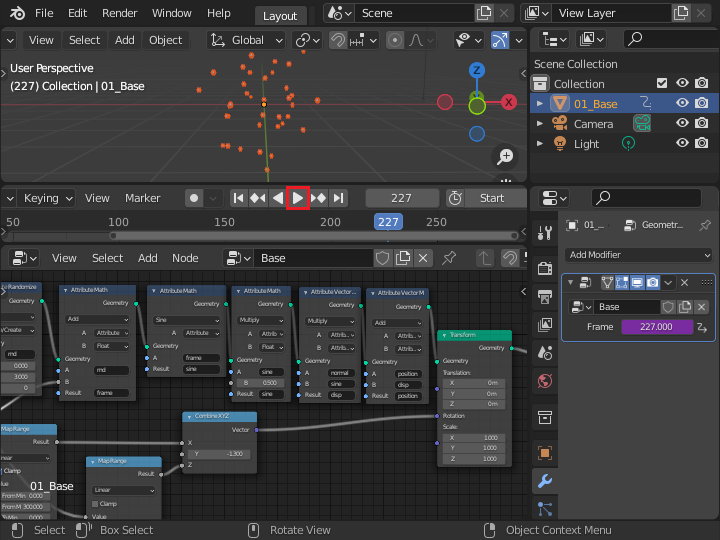
回転して広がる球体の実体(インスタンス)化
これまでに作った回転して運動する点に形状を与えます。 まず、Plane オブジェクトを追加して、ジオメトリーノードを追加します。 このオブジェクトに設定するジオメトリーノードが、「01_Base」オブジェクトで作成した点の運動と、実体(インスタンス)化として作成する形状 (これも球) を接続します。
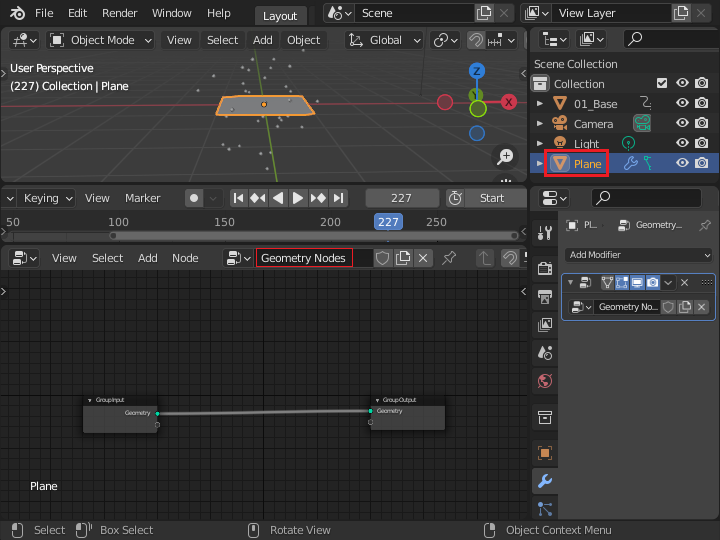
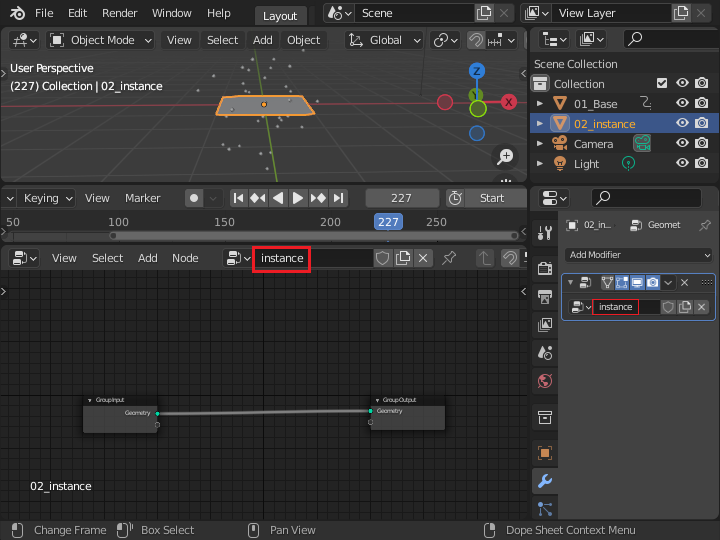
識別できればどのような名前でも構いませんが、ここでは Plane オブジェクトの名前を「02_instance」にして、ジオメトリーノードの名前を「instance」に設定します。
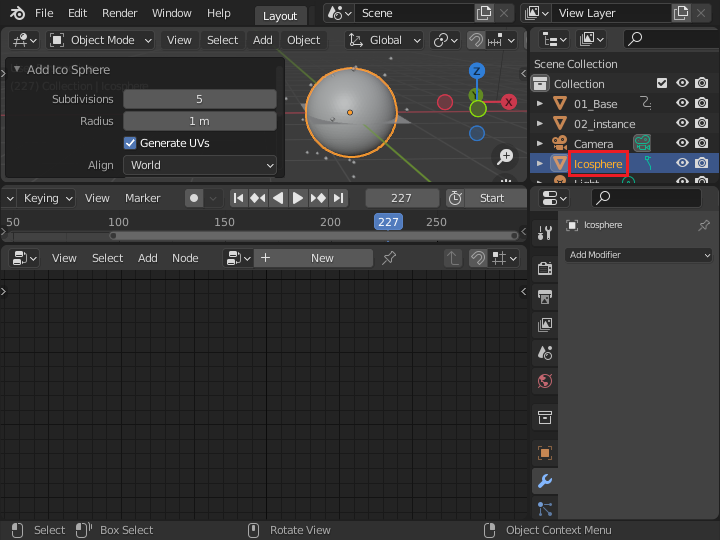
球体の実体 (インスタンス) として、IcoSphere メッシュオブジェクトを追加します。
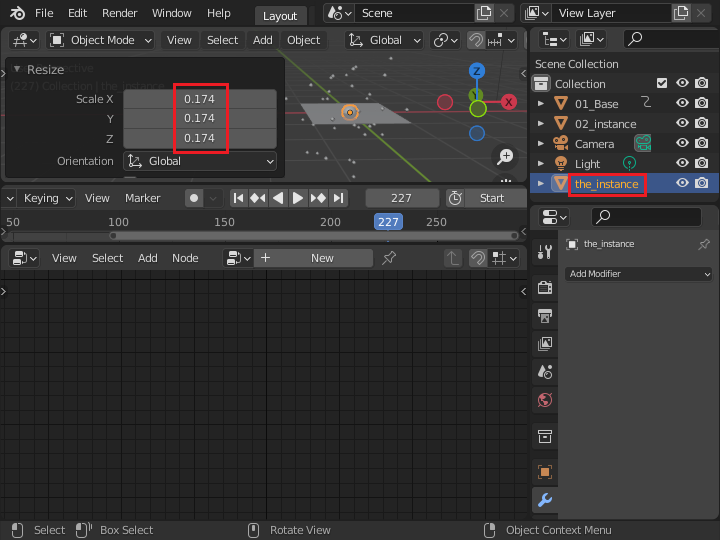
編集モードに変更して、[S]キーで縮小します。 IcoSphere の名前は「the_instance」にしました。
オブジェクトモードで縮小して、「Apply / Scale」で Scale を1.0に戻す方法でも構いません。
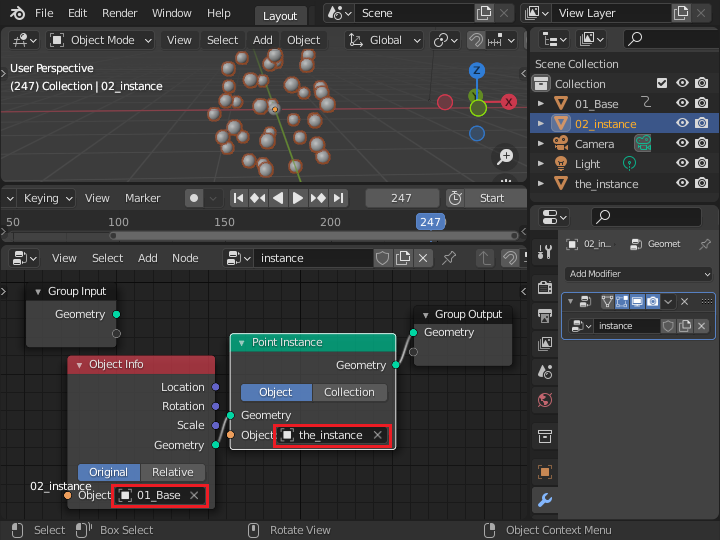
「02_instance」という名前に変更した板オブジェクトのジオメトリーノードに、「Object Info」ノードと「Point Instance」ノードを接続します。
これで、「01_Base」のジオメトリーノードで設定された点の位置に、the_instande の球体が表示され、フレーム数に従って移動するようになります。
中心部で変形する球体
周りを回る小さな球の中心で変形する大きな球体として Ico Sphere を追加します。 なめらかに変形させるため、細分化レベルは 7 に設定します。大きさは 1m のままです。 球体の名前は「03_displace」とします。
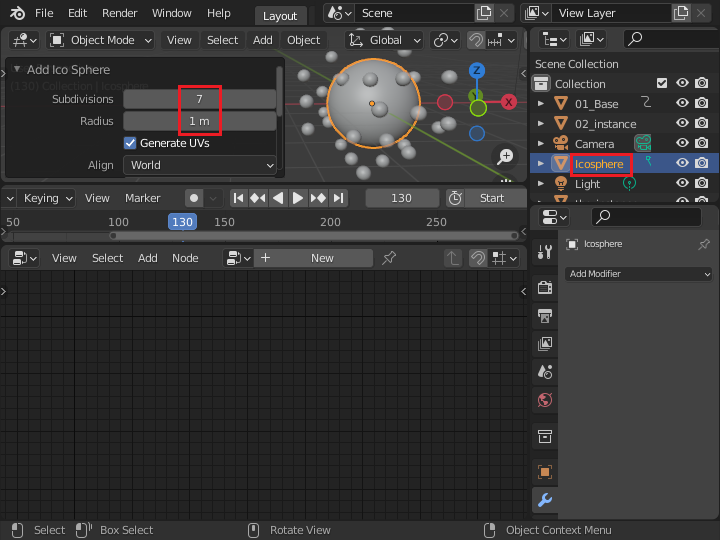
このオブジェクトにもジオメトリーノードを追加して、名前を「Displace」にしました。
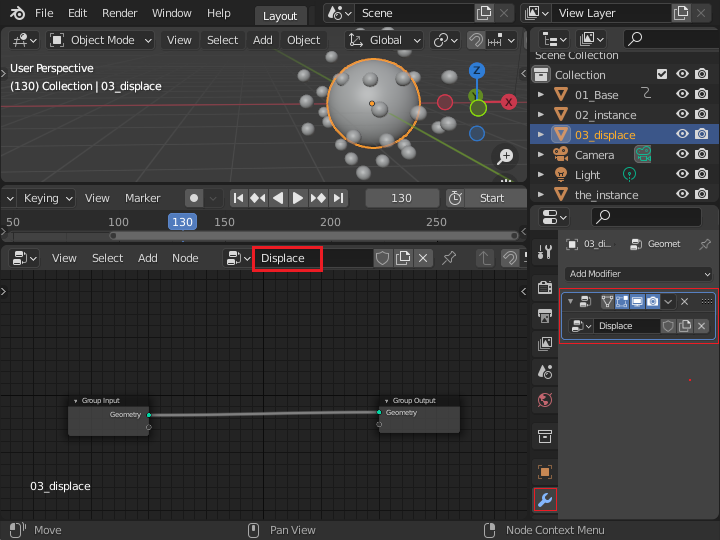
この球体は周りを回る小さい球人の距離に従って変形させるため、追加した「Object Info」ノードにオブジェクトとして「01_Base」を設定します。 距離を求めるため「Attribute Proximity」ノード (近接属性ノード) を追加します。
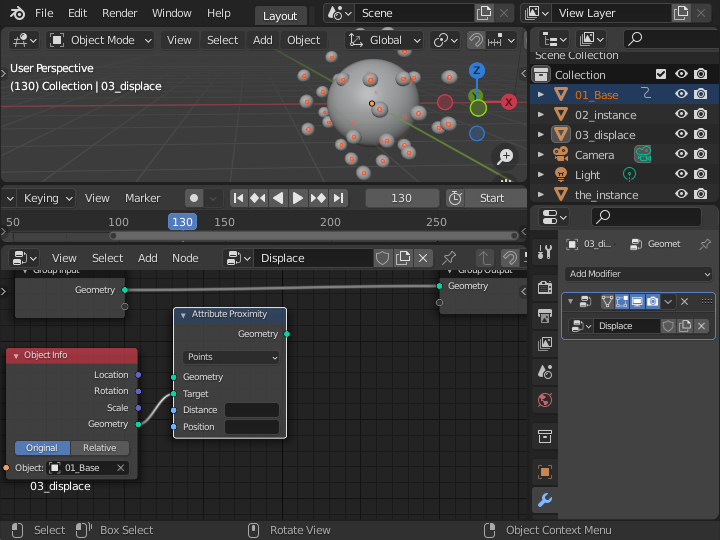
「Attribute Proximity」のGeometryソケットに Group Input ノードを接続し、「Object Info」ノードを Target ソケットに接続します。 Dispance 項目に「dist」という属性を設定します。 これで、「dist」という属性には「01_Base」で設定された点の位置と「03_displace」との距離が設定されます。
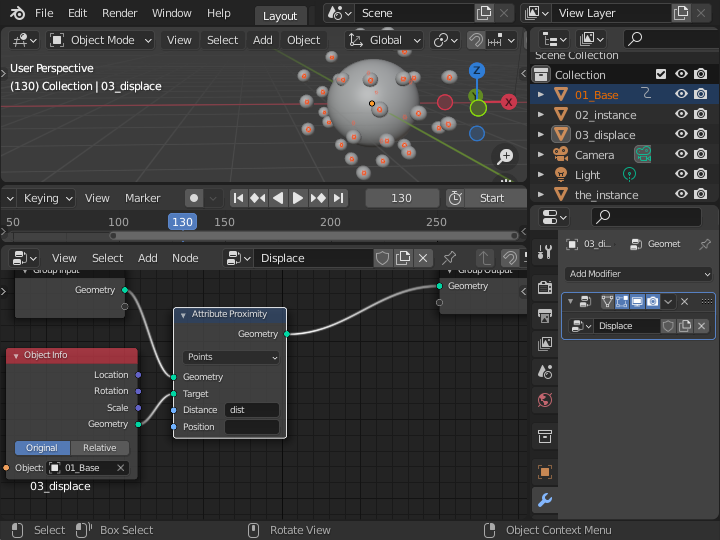
距離がどのように dist に設定されるか確認するために、「Attribute Color Ramp」ノードを接続して、dist の値の大きさに従って色が変化するように、頂点カラーのグループ名となる「Col」属性に渡します。
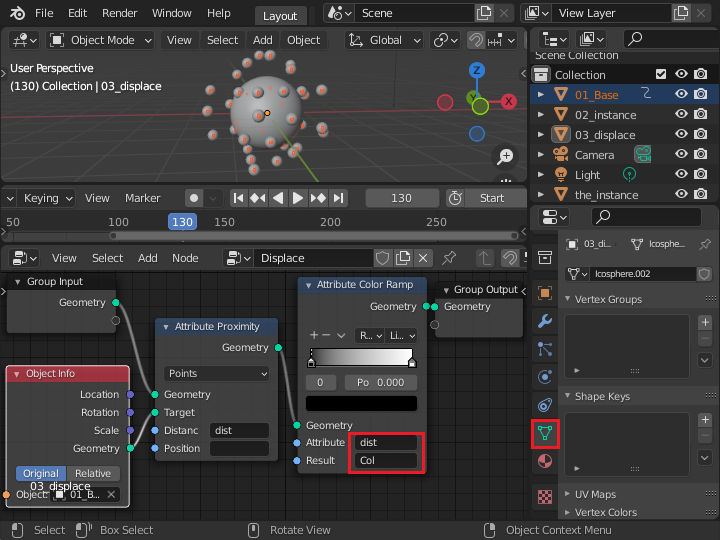
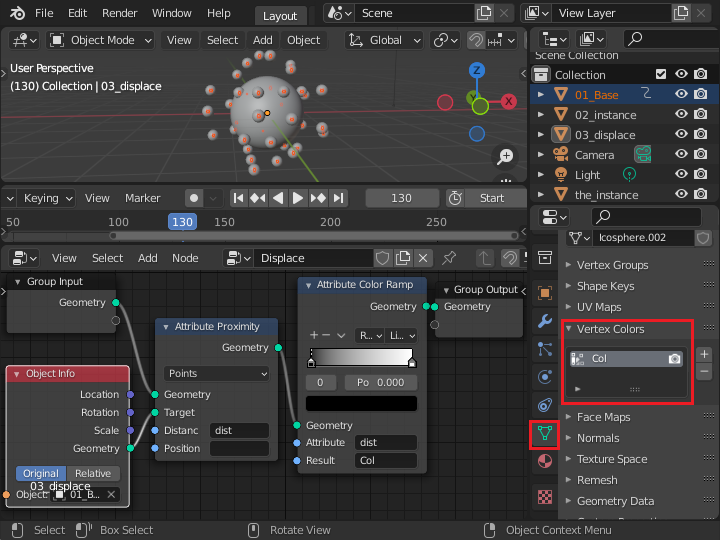
オブジェクトデータプロパティタブの Vertex Colors パネルで [+] を押して Col を追加します。
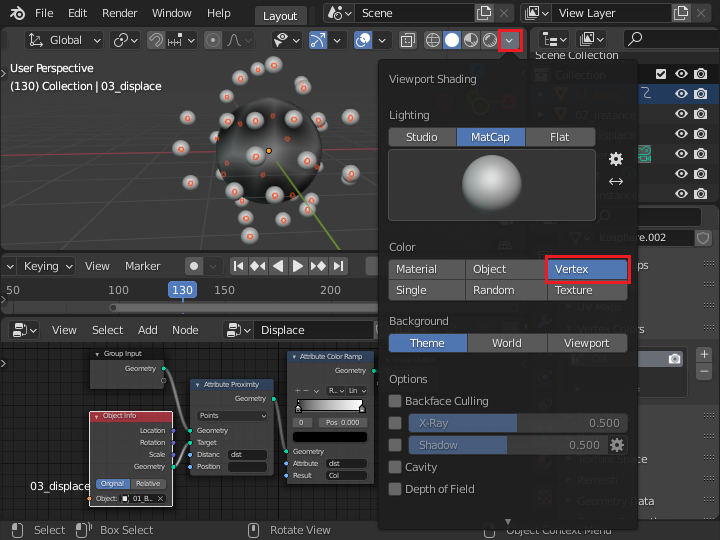
頂点カラーを表示するために、ビューポートのシェイディングの設定で、Color を Vertex に設定します。 小さい球に近い部分の表面の色が黒くなることが確認できます。
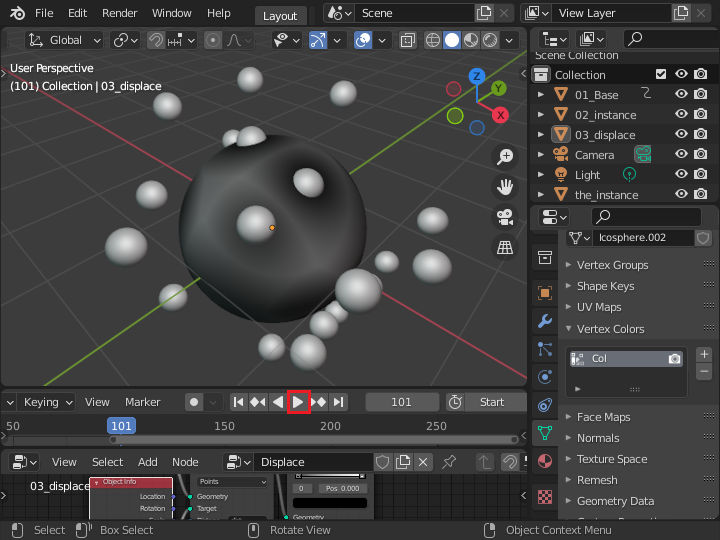
アニメーションを実行すると回転する小さい球の位置に従って、頂点カラーが変化することが確認できます。 距離が近いと dist は 0 となり黒くなります。 距離が遠くなると dist は 1 に近づき白く表示されます。
「Attribute Color Ramp」ノードの色の範囲を変更すると、白と黒の色の比率をコントロールできます。
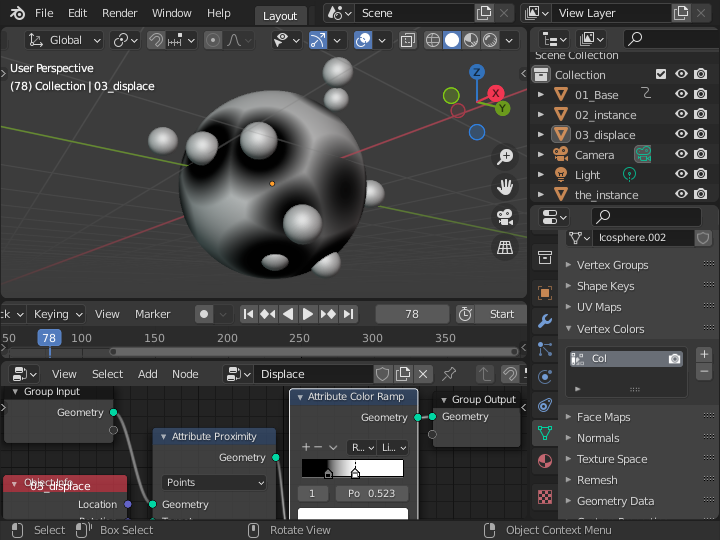
頂点カラーの変化を法線方向の変位量に変換するため、前に説明した「Base」の上側のノードと同様の変換を行います。 まず、「Attribute Separate XYZ」で色を表すグレースケールのRGBから1つの値 (valx) を取り出します。
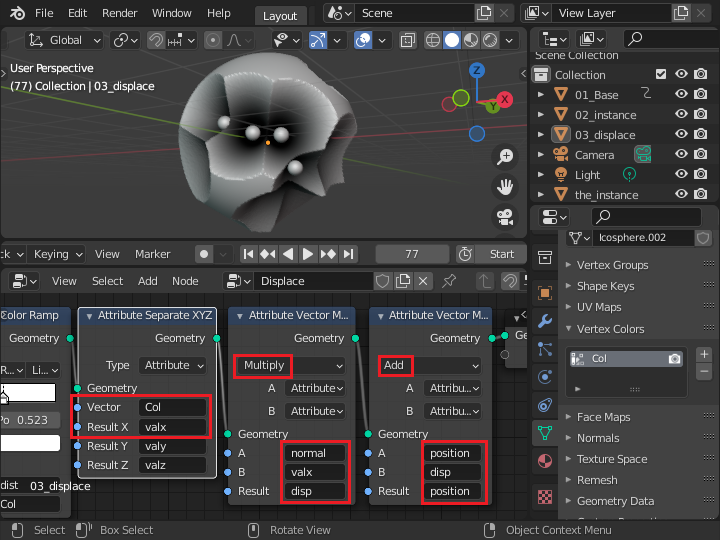
「Attribute Vector Math」ノード2つを使って「position = normal * valx + position」 を計算します。
0 から 1.0 の間の値を取る値を法線ベクトル (normal) に乗算することで、球体の表面の頂点を外側(法線方向)に最大 1.0 が加えられ、図のように小さい球から離れるほど、大きい球体の表面は膨らむことになります。
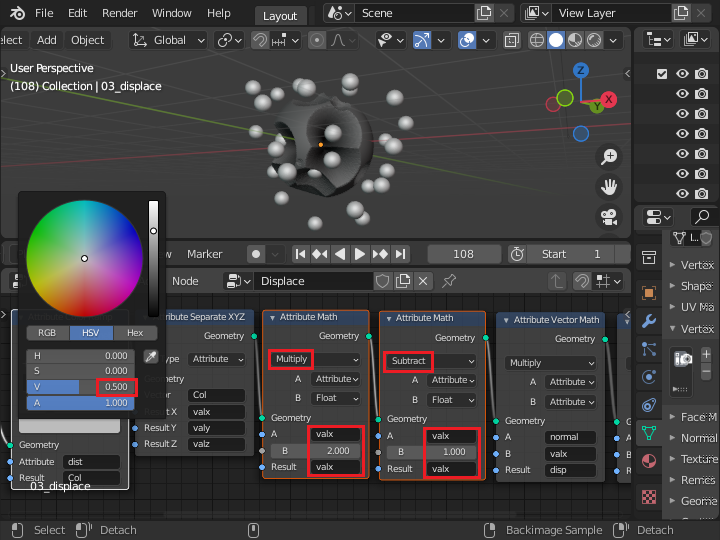
外側に1.0大きくなると大きすぎるため、「Attribute Math」ノード2つを使って「valx = valx * 2.0 - 1.0」を計算し、valx の変化を ±1.0 に変換します。 さらに入力側の「Attribute Color Ramp」ノードで Col の値を 0.5 までに制限すると、元の球体表面のサイズの ±50% の変化になります。
さらに「Attribute Color Ramp」ノードの色の変化を調節することで、ヘリを少しふくらませることができます。
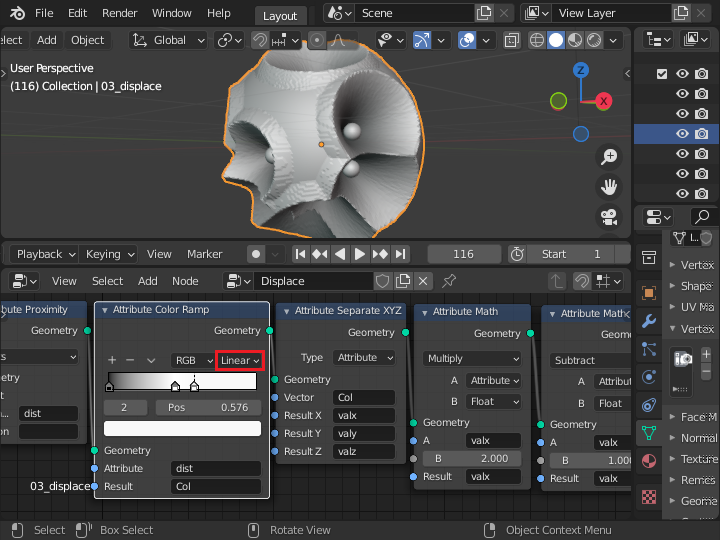
Linear を Ease に変更すると少し丸みを帯びた形状になります。
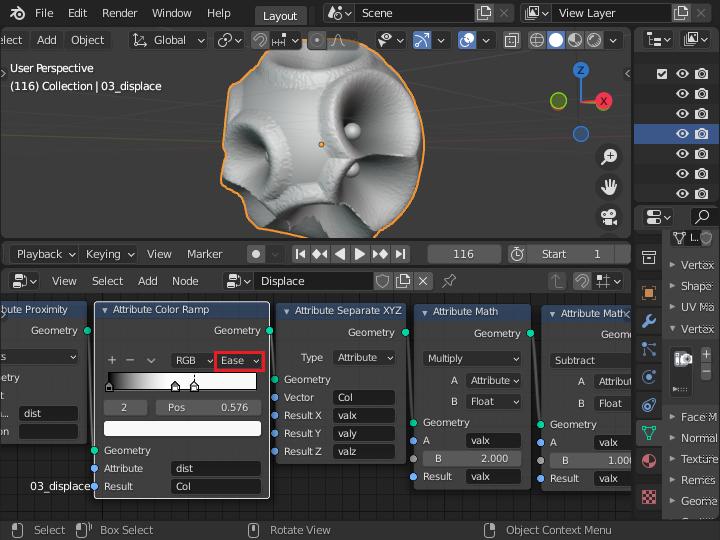
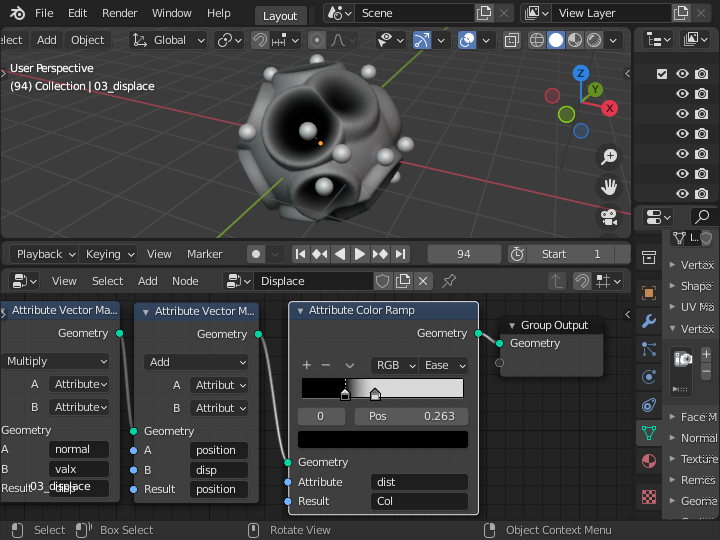
最後に「Group Output」ノードの直前に「Attribute Color Ramp」を追加し、dist を 頂点カラー Col に渡して、変位量とともに頂点カラーも変化するようにします。
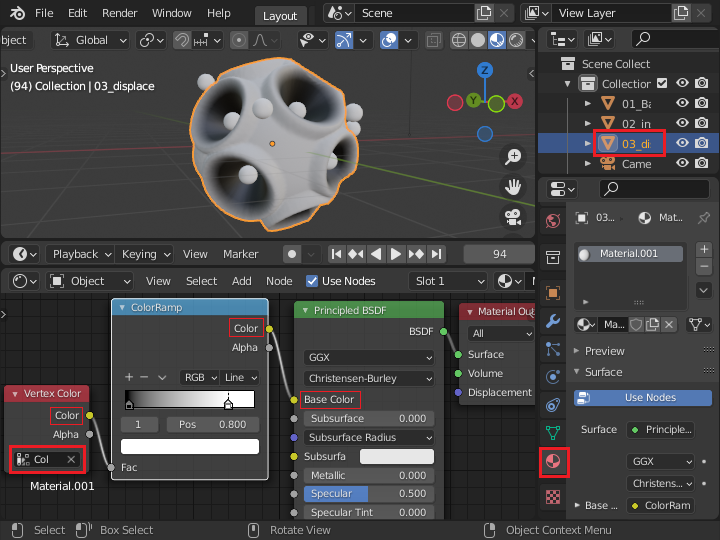
大きい球体のシェーダノードの「Color Ramp」ノードで頂点カラーをマテリアルの色として、細かく色を変化させると、この記事の先頭のスクリーンショットのように表示されます。
頂点カラーの精度
アトリビュートに頂点カラー (Col) を使うと下のようにポリゴン数を増やしても変位量の精度が上がらず、段々な形状となります。
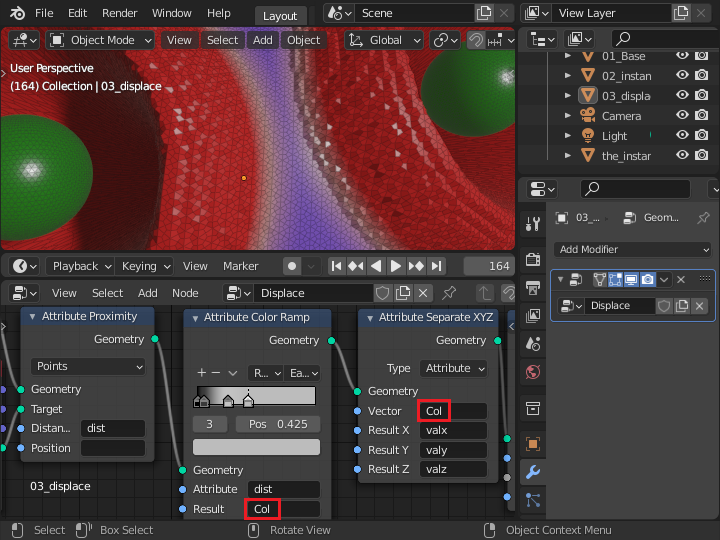
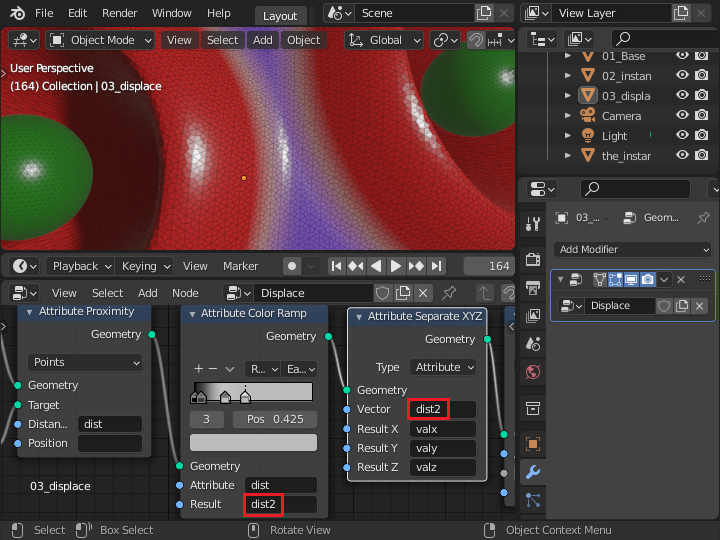
この部分の Col は頂点カラーと関係ないため、任意の名前のアトリビュート(ここでは dist2)を使うとなめらかに変化するようになります。 この例ではフラットシェイディングで描画していますが、スムースシェイディングにするとさらになめらかになります。
動画にしてみました。 右クリックで「コントロールを表示」を選択して再生してください。Ryzen9 5900X と RTX3070 の Ubuntu Linux 20.10 上でこの動画をレンダリングするのにかかった時間は20秒です。 20秒でこのレベルの画像が作れるとはすごい時代になったもんです。